Etude du mouvement elliptique
L'ellipse est depuis le XVIIe siècle, un moyen courant pour déterminer la position des astres dans le ciel ainsi que leur trajectoire souvent très complexe. Les lois de Kepler, entre autres, décrivent le mouvement des planètes autour du Soleil en s'appuyant sur les mesures de Copernic (système héliocentrique en 1543 lié à l'antiquité grecque). En effet, ces trois lois utilisent le mouvement elliptique des planètes du système solaire autour du Soleil qui est l'un des foyers de l'ellipse. Ce mouvement des astres dans un repère héliocentrique sera très important pour la suite de notre TPE.
Mais tout d'abord, commençons par présenter l'ellipse mathématiquement et géométriquement.
L'ellipse est une courbe plane qui fait partie de la famille des coniques. Elle est obtenue par l'intersection du plan avec un cône de révolution lorsque ce plan traverse de part en part le cône. Le cercle est alors un cas particulier de l'ellipse, d'excentricité e=0.
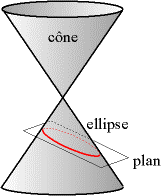
Un petit outil pour vous représenter une ellipse :
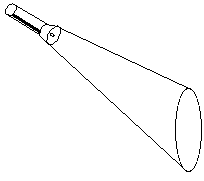
Une lampe-torche crée un cône de lumière : dirigez-le sur un mur plat et vous obtenez une section conique.
Si vous êtes perpendiculaire au mur, celui-ci coupe perpendiculairement l'axe du cône et vous obtenez un cercle lumineux. Inclinez le cône par rapport au mur, le cercle devient une ellipse.
Vous pouvez également utiliser la méthode du jardinier afin de créer une ellipse. Pour la simplifier, vous aurez besoin de deux punaises et d'un fil. Vous lierez les punaises à l'aide de celui-ci et pourrez former une ellipse avec un crayon en utilisant le fil entre les deux punaises.
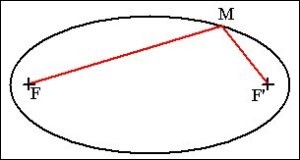
Définition :
L'ellipse est l'ensemble des points M du plan dont la somme des distances à deux points fixes du même plan est une constante donnée. Les deux points fixes F et F' sont appelés foyers.
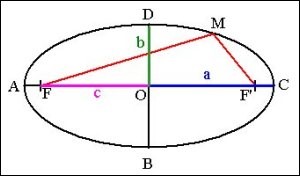
Paramètres :
AC : grand axe
BD : petit axe
O : centre
F et F' : foyers
a : longueur du demi grand axe
b : longueur du demi petit axe
c : distance du centre du foyer
e : excentricité e = c/a (pour une ellipse l'excentricité est comprise entre 0 et 1).
Pour tout point M de l'ellipse MF+MF' = 2a
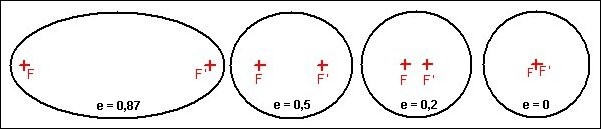
Plus l’excentricité devient faible, plus l’ellipse se rapproche du cercle. Nous pouvons donc définir que, pour une ellipse : 0 <e< 1
Kepler a eu la chance d’étudier la trajectoire de Mars (comme nous verrons ci-dessous) qui est l’une des plus elliptiques du système solaire alors que son excentricité n’est que de … 0,093.
Celle de Mercure est de 0,21 mais la planète est difficilement observable à l'époque et Pluton (e = 0,25) n’était pas encore connue au XVIIème siècle.

Formule :
Dans le repère défini par le grand axe a et le petit axe b de l'ellipse, son équation est telle que :

Application :
Nous utilisons la planète Mars à titre d’exemple. L'aphélie et les périhélies sont deux valeurs faciles à mesurer à l'aide de la parallaxe.

Exemple d'utilisation des équations de l'ellipse :
L'ellipse peut nous aider à calculer de nombreux paramètres astraux. Nous allons ici tenter de calculer la vitesse de révolution de la planète Mars.
Rappelons tout d'abord que le mouvement de révolution est un mouvement de translation périodique, circulaire ou elliptique. La période de révolution, aussi appelée période orbitale, est la durée mise par un astre pour accomplir une révolution complète autour d’un autre astre; par exemple une planète autour du Soleil ou un satellite autour d’une planète.
A l'aide des éléments de l'ellipse, nous tenterons donc de calculer la vitesse de la planète lorsque celle-ci effectue cette trajectoire.

