Les lois de Kepler

Johannes Kepler est né en 1571 et mort en 1630. Il est contemporain de Galilée et vécut entre Copernic et Newton. Ce dernier a d'ailleurs élaboré la plupart de ses lois, notamment celle de la gravitation universelle, grâce aux observations de Kepler.
Kepler était très doué en mathématiques. Son professeur lui enseigna le système héliocentrique de Copernic, qu’il réservait aux meilleurs étudiants. Les autres devaient "se contenter" du système géocentrique de Ptolémée. Kepler devint ainsi un copernicien convaincu. Ses grandes qualités de mathématicien le font remarquer par Tycho Brahé, astronome danois très réputé à l’époque pour la qualité et la précision de ses observations.
Ce fut le premier astronome à construire une carte du ciel avec une très grande précision.
Kepler devint le disciple de Tycho Brahé en 1594, à l’observatoire de Prague.
Kepler remarqua alors que l’orbite de Mars n’était pas un cercle parfait mais plutôt une ellipse. Mais cela impliquait que son maître aurait commis une erreur. Il décida donc de se pencher sur la question et élabora ses fameuses lois.
1. Une orbite elliptique
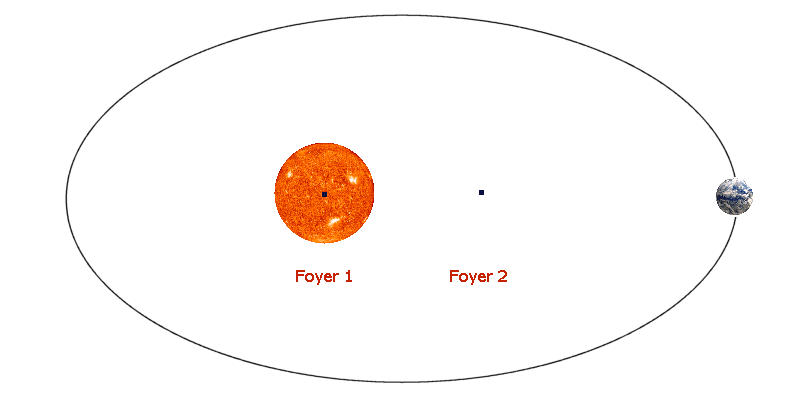
La trajectoire des planètes n’est pas circulaire mais de forme ovale. Elle est appelée ellipse et un des foyers est le Soleil. Kepler publie ce résultat en 1609, enterrant l’ancien dogme de la circularité des orbites.
2. Une relation entre aire et vitesse
Kepler découvre que des secteurs sont balayés pendant des périodes égales par la ligne reliant le Soleil et la planète considérée.
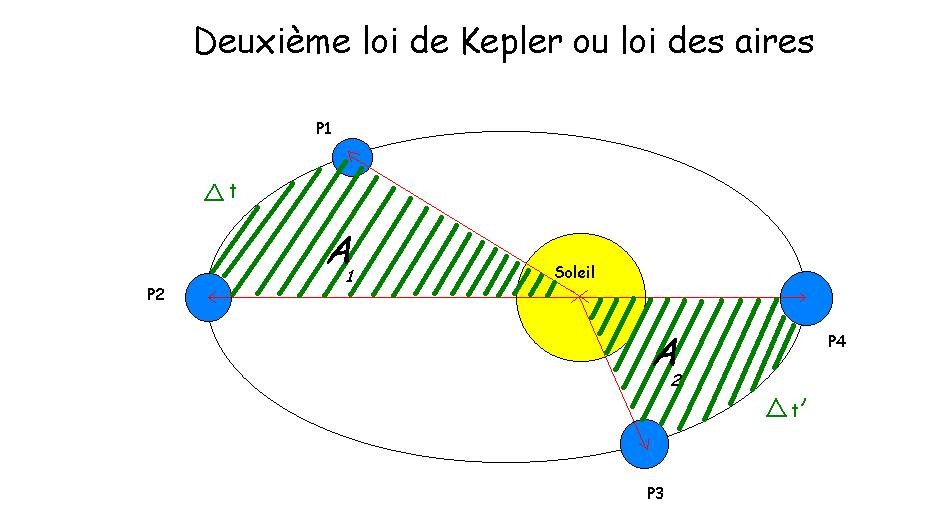
Si delta t et delta t' sont des temps égaux, alors les aires A1 et A2 balayées par le rayon vecteur en ces temps sont égales.
La vitesse d’une planète devient donc plus grande lorsque la planète se rapproche du soleil. Elle est maximale au voisinage du rayon le plus court (périhélie), et minimale au voisinage du rayon le plus grand (aphélie). Cette loi explique, par exemple, la durée des saisons.
En effet, elles n'ont pas toutes la même durée et ce phénomène est dû à la différence de vitesse de la Terre lorsque sa distance au Soleil varie. La Terre passe à son périhélie (environ 147 000 000 km du Soleil) le 4 janvier et à l'aphélie (environ 152 000 000 km) le 5 juillet. La révolution de la Terre étant elliptique, elle obéit à la loi des aires (2e loi de Kepler). Mais la vitesse de la Terre n'est pas linéaire le long de son orbite, la durée des saisons est donc inégale.
C'est pourtant l'inclinaison d’environ 23° 26′ de l’axe de rotation de la Terre qui explique l’existence des saisons et non la petite variation de distance de la Terre au Soleil qui joue un rôle minime et ne pourrait d’ailleurs pas donner d’explication cohérente pour les deux hémisphères. La durée et l’intensité du rayonnement solaire sont effectivement maximales au solstice d’été et minimales au solstice d’hiver. Pourtant, cette loi nous permet de calculer et de comparer les durées des saisons.


Ces lois furent publiées dans Astronomia Nova en 1609, où il fut également le premier à émettre l’hypothèse d’une rotation du Soleil sur son axe.
Il faut replacer cette découverte dans son contexte historique. En effet, le fait que l’orbite d’une planète ne soit plus un cercle parfait était impensable à cette époque. Tout ce qui est dans le ciel étant divin, il ne pouvait y avoir que des mouvements parfaits selon une géométrie parfaite, donc des cercles. Kepler imagine qu’il doit forcément y avoir une harmonie des nombres entre les planètes. Il recherche alors une relation entre le grand axe de l’orbite et la durée de révolution d’une planète autour du soleil. Il énonce alors sa troisième loi avec laquelle il retrouve une harmonie.
3. Une relation entre période et distance
Kepler s’intéresse ainsi aux autres planètes (mouvement de chaque planète autour du soleil). Il montre que le carré de la période de révolution d’une planète (temps nécessaire pour faire un tour) est proportionnel au cube de la taille de son orbite. Elle a permis de déterminer la masse de nombreux corps.


Il est très complexe de justifier cette loi pour une ellipse et les trajectoires effectuées par les planètes sont presque circulaires. Pour alléger les calculs, nous les effectuerons en utilisant une trajectoire circulaire.





